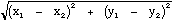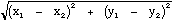A Balanced Introduction to Computer Science and Programming
David Reed
Creighton University
Copyright © 2004 by Prentice Hall
Chapter 5: Data Types and Expressions
Supplemental Material and Exercises
More on expressions and assignments
This chapter contains several exercises in which you traced the execution
of assignments. Tracing code is an excellent way to make sure that you
understand exactly what is going on as expressions are evaluated and values
are assigned to variables. While the exercises in this chapter emphasized
numbers and numeric expressions, similar exercises can be completed to make
sure that you understand string concatenation and the mixed expressions.
EXERCISE 5.11:
Trace the execution of the following JavaScript code and try to predict
its behavior. For each assignment, fill in the boxes corresponding to the
values of the variables -- even those values that aren't changed. For each
write statement, list the output that would be displayed.
| word1 = "foo";
|
| word1
|
|
| word2 = "foo" + "bar";
|
| word1
|
| word2
|
|
|
|
document.write("<p>word1 = " + word1 + ", word2 = " + word2 +
"</p>");
|
|
| word3 = "biz";
|
| word1
|
| word2
|
| word3
|
| word1 = word2 + word3;
|
| word1
|
| word2
|
| word3
|
| word2 = word2 + word2;
|
| word1
|
| word2
|
| word3
|
|
|
document.write("<p>word1 = " + word1 +
", word2 = " + word2 + ", word3 = " + word3 + "</p>");
|
|
Verify your predictions by cut-and-pasting the above code into a Web page
(within SCRIPT tags) and loading that page in the browser.
You do not need to save or print this page.
EXERCISE 5.12:
Trace the execution of the following JavaScript code and try to predict
its behavior. For each assignment, fill in the boxes corresponding to the
values of the variables -- even those values that aren't changed. For each
write statement, list the output that would be displayed.
| num = 1024;
|
| num
|
| msg1 = "x = 0"
|
| num
|
| msg1
|
| msg2 = "num = " + num;
|
| num
|
| msg1
|
| msg2 |
|
|
| document.write("<p>num = " + num + ", " + msg1 + ", " + msg2
+ "</p>");
|
|
| num = num / 2;
|
| num
|
| msg1
|
| msg2
|
|
|
| document.write("<p>num = " + num + ", msg2 = " + msg2 +
"</p>");
|
|
Verify your predictions by cut-and-pasting the above code into a Web page
(within SCRIPT tags) and loading that page in the browser.
You do not need to save or print this page.
EXERCISE 5.13:
Consider the task of swapping the values of two variables. For example,
if num1 was assigned the value 12 and num2 was
assigned -9.3,
then after executing some JavaScript statements we would like for their
values to be reversed.
Do the following two statements accomplish this task? If not, would
reversing the two statements result in the desired swap? Explain.
num1 = num2;
num2 = num1;
Give several JavaScript statements that correctly swap the values
of num1 and num2. Hint: would a third
variable be useful?
More on parseFloat
Several exercises in this chapter demonstrated the use of the predefined
parseFloat function to convert a string of digits into the
corresponding number. In particular, the parseFloat function
is needed whenever a numeric value is to be read in from the user, since
the prompt function always returns a string value. To read in a
numeric value, two lines of the following form are required:
variableName = prompt("Enter a value...", "");
variableName = parseFloat(variableName);
The first line reads in the user's input as a string value and stores it
in the variable. The second line then calls the parseFloat function
with that string as input to convert it to a numeric value, then reassigns
that number back to the variable.
Equivalently, the two statement could be combined into one, where the
output of the prompt function is sent directly as input to the
parseFloat function.
variableName = parseFloat(prompt("Enter a value...", ""));
If you prefer it, you may use this abbreviated notation when reading in and
storing number values.
EXERCISE 5.14:
In the late 70's, Lorne Greene (of Bonanza fame) starred in a series of dog
food commercials where he referred to the age of dogs in relative human
years. Due to their shorter life span, one year in a dog's life is
equivalent to approximately 7 human years. Create a Web page named
dogage.html that prompts the user for the age of their dog, and
then displays that age in human years. For example:
Your dog is 10 years old -- that's 70 to you and me!
EXERCISE 5.15:
Trace the execution of the following JavaScript code and try to predict its behavior.
Be sure to differentiate between string values (using quotes) and numeric values in
the memory cells. Assume the user enters the value 1024 at the prompt.
| x = prompt("Enter a number:", "");
|
| x
|
| document.write("<p>Double " + x + " is " + (2 * x) +
"</p>")
|
|
| document.write("<p>Double " + x + " is " + (x + x) +
"</p>")
|
|
| x = parseFloat(x);
|
| x
|
| document.write("<p>Double " + x + " is " + (x + x) +
"</p>")
|
|
Verify your predictions by cut-and-pasting the above code into a Web page
(within SCRIPT tags) and loading that page in the browser. You do not
need to save or print this page.
Remainder
In addition to the traditional mathematical operators, JavaScript provides
an additional operator '%' known as the remainder operator. When applied to
two numbers, the remainder operator computes the number that would remain
after dividing the first number by the second. For example,
(7 % 2) would evaluate to 1, since 2 divides 7 three times
with a remainder of 1. Likewise, (15 % 3) would evaluate
to 0, since 3 divides 15 five times with a remainder of 0.
The remainder operator is especially useful for problems in which a value
must be broken down into pieces of varying sizes. For example, some computers
applications allow you to determine how many seconds have lapsed between
two events. While this is useful for timing short intervals, intervals of
several minutes or even hours are difficult to comprehend when displayed
as seconds. To most people, it is not obvious just how long 12345 seconds
is. When broken into hours and minutes, however, this interval is easy to
comprehend: 3 hours, 25 minutes, and 45 seconds.
Assuming the number of seconds is stored in a variable named
seconds, the following JavaScript code suffices to break those
seconds into hours, minutes and seconds.
hours = Math.floor(seconds / (60*60));
seconds = seconds % (60*60);
minutes = Math.floor(seconds / 60);
seconds = seconds % 60;
The first assignment computes the number of hours in the specified interval
by first dividing the seconds by the number of seconds in an hour, and then
rounding down (to eliminate any partial hours). Then, the remainder operator
is used in the second assignment to reset seconds to be what remains after
taking away the hours. For example, dividing 12345 by (60*60) yields
3.42916667, which is rounded down to 3 full hours by the Math.floor
function. The remainder after dividing 12345 by (60*60) is 1545, the number
of seconds remaining after the three hours have been removed. Similarly, the
next two assignments compute the number of minutes and then the remaining
seconds after minutes have been taken away. Continuing this example,
dividing 1545 by 60 yields 25.75, which is rounded down to 25 full minutes.
The remainder after dividing 1545 by 60 is 45, the number of seconds
remaining after the 25 minutes have been removed.
EXERCISE 5.16:
Create a Web page named times.html that prompts the user for a
number of seconds and stores that number in a variable. Your page should
use the above assignments to break that number of seconds into hours,
minutes, and seconds and display those values. For example, if the
user enters 12345 at the prompt, the page should display:
That's equivalent to 3 hours, 25 minutes, and 45 seconds.
Use your page to convert each of the following time intervals.
20 seconds
500 seconds
86400 seconds
123456 seconds
EXERCISE 5.17:
Add code to your times.html page so that the number of days is
also taken into account when breaking up intervals. That is, the number of
seconds should first be broken into a number of days (using code similar to
above), then hours, minutes and seconds as before.
Use your page to convert each of the following time intervals.
86399 seconds
86400 seconds
123456 seconds
1000000 seconds
Random integers
Suppose we wanted to simulate the roll of a single six-sided die.
The following expression can be used to generate a random integer in the
range 1 through 6, inclusive.
Math.floor(6*Math.random()) + 1
Since the call Math.random() returns a number in the range [0,1), multiplying
that number by 6 will produce a number in the range [0,6). Taking the floor
will yield an integer in the range 0 to 5, inclusive. Finally, adding 1 to
that yields a random integer between 1 and 6.
EXERCISE 5.18:
Generalize the above expression so that it makes use of two variables
low and high, evaluating to a random integer in the range
low to high. Test your expression on paper by considering
the smallest possible value (obtained when Math.random() returns 0)
and the largest possible value (obtained when Math.random() returns
a number very close to 1). Note: you may assume that
low <= high.
EXERCISE 5.19:
Using the formula that you devised in the previous exercise, create a
Web page named range.html that prompts the user for two integers,
the low and high numbers in a range. The page should then generate and
display a random integer in that range.
EXERCISE 5.20:
It may surprise you to learn that random events such as coin flips, dice rolls, and
roulette wheel spins are central to many computer science applications, such as
cryptography and database management. While events such as these are random in
nature, their behavior over the long run is predictable and so can be used to
construct deterministic solutions to complex problems. Problem solutions that use
such random events are known as Monte Carlo methods, named after the city
famous for its casinos.
For example, if you generate a large number of random points within a square, and
count the number of points that lie within an inscribed circle, you can estimate the
ratio between the areas of the circle and square. Given this ratio, it is possible to
estimate the value of PI.
|
PI = 4*(area of inscribed circle/area of square)
|

|
Create a Web page named distance.html that performs a simplified version
of this task: generating a single random point in the square and determining its
distance from the center. Assuming the square has its center at (1,1) and sides of
length 2, a point will lie inside the inscribed circle as long as its distance from
(1,1) is no more than 1. For example,
random point: (1.6242531588851183, .9896060308809078)
The distance between this point and (1,1): .6243396839638639
Helpful hints: In order to generate a random point (x, y) in the square, you
will need to generate two random numbers in the range [0...2) for x and y. This can be
accomplished using the expression 2*Math.random(), as demonstrated in the
previous exercise. The following formula can be used to calculate the distance between
arbitrary points (x1, y1) and (x2, y2):