Function names vs. function calls

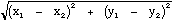
A common mistake made by beginning programmers is to specify only the function name when a call to that function is intended. For example,

While the intent might be to call the function, FahrToCelsius is not recognized as a function call without parentheses, e.g., FahrToCelsius(212). Even if the function has no inputs, parentheses must be provided, e.g., Math.random().

It is interesting to note that forgetting the parentheses in a function call will not necessarily produce an error. Technically speaking, the name of a function is a variable just like any other. The value of a function name is a string that contains the full definition of the function itself. As is the case with any variable, this value can be displayed or compared to another value. For example, if the FahrToCelsius function were defined as in Chapter 7, the write statement above would actually display the definition of that function.

EXERCISE 7.10:    Will mistakes such as the one described above (listing only the function name instead of a call to that function) ever produce an error in JavaScript code? If so, give an example. If not, explain why.

EXERCISE 7.11:    For user-defined functions, the definition of the function can always be reviewed by displaying the function name (as demonstrated above). Does this same option apply for predefined JavaScript functions? That is, could you review the source code for Math.sqrt by displaying the function name? Try it and report the results.

More on parameters and local variables

In addition to shortening pages by consolidating redundant code, the use of functions can produce code that is simpler to modify. For example, consider the Old MacDonald page. Since every verse of the song is now displayed using the same function, changes to that one function will automatically affect all verses. Encapsulating the general task of displaying a verse in a single function means that changes must only occur in that one place, and consistency across all verses is assured.

EXERCISE 7.12:    Similar to the modification you made to your Old MacDonald code in Chapter 4, add a variable to your newMac.html page so that that defines the spelling of the refrain for the verse (e.g., "E-I-E-I-O" or "Eeyigh-Eeyigh-Oh"). This variable should be used when displaying the verse, so that changing the value assigned to that variable changes the refrain that is displayed. Note: you should be sure to declare that variable at the top of the function to make it local to the function.

EXERCISE 7.13:    Consider the incomeTax function discussed in Chapter 7. Most workers have part of their paychecks withheld every month to apply towards their income tax. When their taxes are filed at the end of the year, the total amount withheld during the year is subtracted from their computed tax to determine the amount that they owe. Modify the incomeTax function to have a third input, the amount withheld. The function should compute the amount owed by the taxpayer (stored in a variable named taxOwed) and return that value. Be sure to add your new variable to the variable declarations so that it will exist only inside the function. Similarly, modify your page so that it also prompts the user for the amount withheld and calls the function accordingly.

Use your page to determine the amount a person would owe with:

income = 100000.00 itemized = 12017.50 withheld = 10000.00 income = 42500.00 itemized = 8900.99 withheld = 6250.75 income = 13267.45 itemized = 14000.00 withheld = 0.00

More on libraries

As was demonstrated by the random.js library, useful function definitions can be grouped together in a library file and then loaded into any page that might need those functions. You may find that as you write more programs, some functions will be revisited over and over. In such cases, you might consider defining your own library file to make function reuse easier.

EXERCISE 7.14:    If you were working for a weather service, converting temperatures back and forth from Fahrenheit to Celsius might be a common task. Define a library file named convert.js that contains your definitions of the functions FahrToCelsius and CelsiusToFahr. Then, modify your convert.html page to make use of this library.

EXERCISE 7.15:    Extend your convert.js library by adding functions for converting measurements to and from Metric. First, define functions for converting from inches to centimeters, and vice versa (1 in = 2.54 cm). Once you have these functions defined, you can use them to help convert from feet to meters, and vice versa (1 ft = 12 in, 1 m = 100 cm). Finally, use those functions to help convert from miles to kilometers, and vice versa (1 mi = 5,280 ft, 1 km = 1,000 m).

Modify your convert.html page to test your new conversion functions.

Consider the task of simulating the rolling of two six-sided dice. This could be accomplished by evaluating a complex expression involving calls to Math.random and Math.floor. Using the abstraction provided by the RandomInt function from the random.js library, however, this task is greatly simplified. To obtain the sum of two dice rolls, you can simply call the randomInt function twice and add the returned values:

EXERCISE 7.16:    Evaluate and display the value of this expression 10 times, and report the results. You should obtain numbers between 2 and 12, with a greater likelihood of obtaining numbers in the middle of the range. Do your experiments meet these expectations?

This same incremental approach to complexity applies in programming as well. When the RandomInt function was defined, it made use of the Math.random and Math.floor functions that are predefined in JavaScript. Once this new function was defined, you were able to use it to simulate the roll of two six-sided dice by evaluating the expression RandomInt(1,6) + RandomInt(1,6). Since dice rolls are useful in many applications, you will be performing numerous dice simulations throughout this course. As such, it will prove useful to build upon the RandomInt abstraction to define define yet another level of abstraction.

EXERCISE 7.17:    Define a function called DiceRoll that simulates the rolling of two dice. It should have one parameter, representing the number of sides on the dice. It should simulate the dice rolls by calling RandomInt twice and returning the sum of the two rolls.

Test this function in a Web page that generates and displays random dice rolls.

EXERCISE 7.17:    Reimplement your pick4.html page from Chapter 5 using the RandomInt function from random.js. That is, each ball for the Pick 4 lottery should be selected by calling the RandomInt function, with the maximum ball number specified by the user.

Function calling sequence

Whenever a function is called, a specific sequence of events takes place. If you understand this sequence, it should be possible to trace the execution of any function and ascertain its behavior. For example, consider the following page that computes the distance between two points using the following formula:

<html> <!-- newdist.html Dave Reed --> <!----------------------------------------------------> <head> <title>Point Distance</title> <script type="text/javascript"> function Distance(x1, y1, x2, y2) // Assumes: (x1,y1) and (x2,y2) are coordinates // Returns: the distance between the two points { var temp1, temp2; temp1 = Math.pow(x1 - x2, 2); temp2 = Math.pow(y1 - y2, 2); return Math.sqrt(temp1 + temp2); } </script> </head> <body> <script type="text/javascript"> x = 3; y = 4; d = Distance(0, 0, x, y); document.write("The distance is between (0,0) and " + "(" + x + ", " + y + ") is " + d); </script> </body> </html>

When the distance function is called in the BODY of the page, the following events occur:

1. The inputs to the function are evaluated first, with the variables x and y evaluating to 3 and 4, respectively.
2. Next, execution shifts to the Distance function to perform the actual computation.
3. Within the function, new memory cells are allocated for the parameters and local variables. In the case of parameters, the associated memory cells are assigned the values of the corresponding inputs from the call, i.e., the parameters x1, y1, x2, and y2 are assigned 0, 0, 3 and 4, respectively.
4. The statements in the function are executed in order, assigning temp1 the value 9 and temp2 the value 16.
5. When the return statement is reached, the expression in the statement is evaluated, yielding 5.
6. After computing the return value, the execution of the function is over. Since the parameters and local variables exist only inside the function itself, the memory cells associated with these variables are deallocated, i.e., made available for other uses.
7. Once the memory cells have been freed, 5 can be returned as the value of the function call. In this case, the value 5 replaces the function call in the assignment, and so d is assigned 5.

1. The arguments in the function call are evaluated.
2. Execution shifts to the function being called.
3. Memory cells are allocated (created) for each parameter and local variable in the function, and in the case of parameters, the values of the corresponding inputs are assigned to the memory cells.
4. The statements in the body of the function are executed in order.
5. When a return statement is encountered, the expression is evaluated.
6. Memory cells associated with the parameters and local variables are deallocated (destroyed).
7. Upon return, the value of the expression in the return statement replaces the function call in whatever expression it appears in.

EXERCISE 7.19:    Similar to the example above, trace the sequence of events that occur as a result of the call to Distance in the following write statement: document.write( Distance(2, 1+1, 3+2, 6) );

Cut-and-paste the newdist.html text into a new Web page and modify the page to verify your final answer.

EXERCISE 7.20:    What would happen if you placed a statement after the return statement in a function? For example, what if you put another return statement immediately after the existing one in Distance? return "??????"; Would this additional statement affect the behavior of the function? Why or why not? Verify your answer by adding this statement to the Distance function and calling it as before.

JavaScript variables that appear in the BODY of a Web page are known as global variables since they can be accessed from anywhere, including functions defined in the HEAD. Through parameters and local variables, a function has the ability to create variables that exist and are visible only inside that function. For example, within the Distance function, the parameters x1, y1, x2, and y2 are accessible, as are the local variables temp1, and temp2. The global variables x and y are also accessible within the function, but are not actually used here.

Since each function in a page can have its own local variables, it is possible to have the same variable name refer to distinct memory cells. For example, suppose the local variables temp1 and temp2 in the function were instead named x and y (identical to the global variables in the BODY). While this might be confusing to the reader, the browser is not confused at all. The global variables named x and y are separate from the local variables x and y, with the local variables being accessible only from within the Distance function. Using the subscript notation introduced in the chapter, we can think of the local variables as x_Distance and y_Distance, and the global variables as as x_BODY and y_BODY. Assignments made to x and y within the function would affect the local variables only (x_Distance and y_Distance), leaving the global variables (x_BODY and y_BODY) untouched.

EXERCISE 7.21:    Verify that global and local variables behave as described above by modifying the newdist.html page. Rename the local variables in the function x and y and verify that the output of the page is unchanged.

Once again, the idea behind functions is to build up independent units of abstraction. We would like to be able to call a function and not worry about how it works. Declaring variables inside a function to be local is instrumental in achieving this level of abstraction. If all variables used inside a function are declared to be local, then the execution of that function is not affected by nor does it affect any external variables. If functions access and change global variables, however, the results may be difficult to predict or control. For example, suppose that the variables in the Distance function were named x and y but not declared to be local (using the var declaration). If that were the case, then assignments to those variables would affect the global variables that appear in the BODY.

EXERCISE 7.22:    To demonstrate this undesirable effect, modify your newdist.html page further by commenting out the variable declarations in the Distance function. That is, place double slashes '//' at the front of that line of code. Assuming you still have the variables in the function named x and y, what output is produced by this modified page? Why is this different from the last exercise?